Cláudio Dias, Head of Ground Engineering & Tunnelling at AYESA – Blog Bentley Systems
Introduzione
Questo è il secondo articolo dedicato alla modellazione del Metodo Tradizionale di Madrid (MTM) con PLAXIS 2D e 3D.
Per ulteriori dettagli sul metodo, si rimanda al webinar (Traditional Tunnelling Method: Application of MTM with PLAXIS 2D/3D) e al primo articolo del blog (PLAXIS 2D – Traditional Tunnelling Method: Application of MTM).
In questo contributo viene presentato un approccio tridimensionale (3D) al Metodo Tradizionale di Madrid. Tuttavia, la realizzazione di un modello 3D non è sempre possibile, a causa di vincoli di budget o tempi di progetto.
Questo articolo ha tre obiettivi principali:
Migliorare gli approcci di progettazione esistenti, introducendo un nuovo metodo 2D basato sulla calibrazione con un modello tridimensionale di interazione suolo-struttura (SSI);
Fornire un supporto progettuale più informato nei casi in cui un modello 3D non sia disponibile;
Promuovere progetti più sostenibili, mantenendo comunque elevati standard di sicurezza e qualità.
Modelli di Interazione Suolo-Struttura (SSI)
Per prima cosa, è necessario creare due modelli:
uno tridimensionale (3D) e uno bidimensionale (2D) di interazione suolo-struttura (SSI), basandosi sul primo.
Per la generazione di entrambi i modelli è stato utilizzato il programma di calcolo agli elementi finiti PLAXIS, nelle versioni PLAXIS 3D e PLAXIS 2D, rispettivamente.
La geologia utilizzata per entrambi i modelli è già descritta nel Primo Blog (PLAXIS 2D – Traditional Tunnelling Method: Application of MTM) ed è riassunta nella tabella sottostante.
Tabella 1 – Riassunto della stratigrafia dei modelli
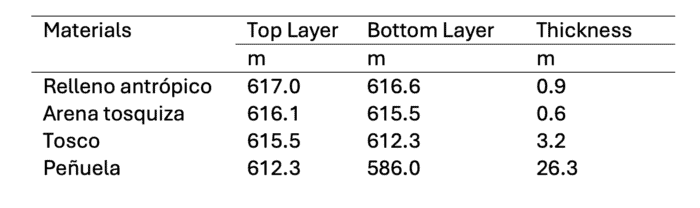
Figura 2: Modello 3D di Interazione Suolo-Struttura (SSI)
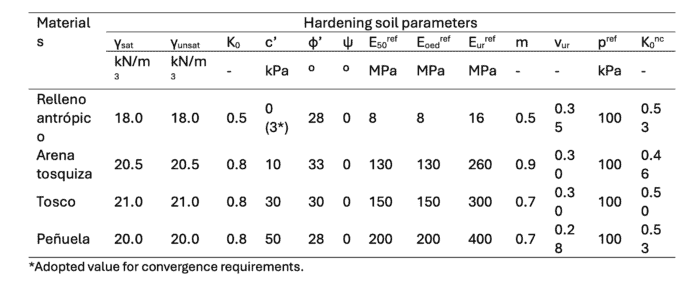
I modelli costitutivi utilizzati per rappresentare il comportamento del terreno sono descritti nel primo articolo del blog e sintetizzati nella tabella seguente.
Tabella 2: Parametri del terreno – Modello Hardening Soil
Modello 3D di Interazione Suolo-Struttura (SSI 3D)
Il modello tridimensionale di interazione suolo-struttura (SSI) sviluppato in PLAXIS 3D presenta dimensioni pari a 40 metri per 60 metri in pianta e 31 metri di profondità, come mostrato nell’immagine precedente.
Il modello è composto da oltre 162.000 elementi finiti, e il rivestimento del tunnel è stato modellato come elementi volumetrici, con piastre fittizie (dummy plates) posizionate nei loro centroidi, per facilitare l’estrazione delle forze interne necessarie alla progettazione strutturale.
Le immagini seguenti mostrano in maggior dettaglio gli elementi volumetrici utilizzati per la modellazione del rivestimento in calcestruzzo non armato, nonché gli elementi strutturali impiegati in questo modello 3D SSI, tra cui:
le travi longitudinali in acciaio (waler beams),
le assi in legno (timber planks),
e i puntelli in legno (timber struts),
utilizzati per simulare le opere provvisorie di sostegno del terreno durante lo scavo, prima dell’installazione del rivestimento permanente in calcestruzzo.
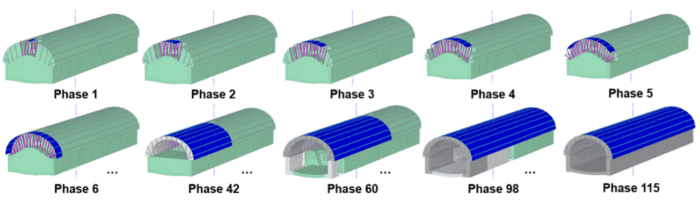
Infine, il modello riproduce la complessa sequenza costruttiva del Metodo Tradizionale di Madrid, articolata in sei fasi indipendenti per l’escavazione di un singolo avanzamento della volta (crown), con una lunghezza di 2,5 metri per tratto.
Nel complesso, il modello rappresenta la costruzione di 16 avanzamenti consecutivi (16 × 2,5 m = 40 metri), includendo anche la realizzazione delle pareti laterali e dell’invert (pavimento del tunnel), per un totale di 115 fasi di calcolo complessive.
Calibrazione
L’obiettivo della calibrazione è ottenere un insieme di fasi di calcolo che rappresentino in modo accurato il comportamento del Metodo Tradizionale di Madrid (MTM), riproducendo il comportamento tridimensionale richiesto all’interno di un’analisi bidimensionale (2D).
Questo approccio implica una semplificazione del modello di calcolo, poiché il problema viene analizzato come un caso a deformazione piana (plane strain) in 2D.
Tale semplificazione comporta che le fasi del processo costruttivo non possano essere idealizzate direttamente, ma richiedano uno studio basato su un modello tridimensionale per poter rappresentare in modo realistico l’effetto complessivo dello scavo e del sistema di sostegno.
Per rappresentare correttamente il comportamento reale in un modello 2D, è necessario calibrare l’effetto di confinamento che si manifesta nei modelli tridimensionali.
Questa calibrazione viene eseguita utilizzando il parametro numerico Mstage di PLAXIS, il quale controlla il grado di deconfinamento dello scavo, ovvero il rapporto tra le tensioni sbilanciate che devono raggiungere l’equilibrio in una determinata fase del modello.
Pertanto, la principale variabile di analisi è stata il livello di rilassamento che il terreno può subire in ciascuna fase di calcolo durante le operazioni di scavo.
Sono state inoltre introdotte alcune ipotesi basate sull’esperienza e sulla conoscenza del metodo costruttivo, tra cui:
È stata creata una fase di sostegno virtuale, per simulare il comportamento del terreno durante lo scavo della volta (top heading).
Senza questa fase, le deformazioni osservate nel modello 3D non sarebbero state riprodotte nello stesso modo, a causa della distanza dalla fronte di scavo e dell’effetto di arco longitudinale del terreno.È stato imposto che il livello di rilassamento durante lo scavo delle panche laterali fosse identico, al fine di garantire la simmetria del modello.
Il processo di calibrazione è stato condotto confrontando:
il livello di cedimento superficiale del terreno,
e i movimenti verticali della volta (crown)
in ciascuna fase di calcolo dei due modelli (2D e 3D).
Dopo aver ottenuto risultati di deformazione coerenti, si è verificato che anche le forze interne agenti sulla struttura del tunnel risultassero comparabili in entrambi i modelli.
I risultati ottenuti da questa calibrazione vengono presentati nelle sezioni successive.
Cedimenti del terreno
Il valore massimo dei cedimenti superficiali nella fase finale del calcolo risulta pari a:
7,74 mm per il modello 3D,
e 7,73 mm per il modello 2D.
Per quanto riguarda la variazione di questi spostamenti verticali durante le diverse fasi di calcolo, dai grafici seguenti si osserva che il cedimento ottenuto nella prima fase, la più critica, rappresenta circa il 40% del valore finale raggiunto in entrambi i modelli — più precisamente:
41% nel modello 3D,
42% nel modello 2D —
corrispondenti in entrambi i casi a un cedimento di circa 3,2 mm.
Durante la fase di getto del calcestruzzo della volta (crown), i cedimenti accumulati raggiungono circa il 72% in entrambi i modelli, ovvero 5,6 mm.
Successivamente, nella fase di scavo della parete sinistra, il valore accumulato ammonta a:
91% (7,1 mm) per il modello 3D,
e 88% (6,8 mm) per il modello 2D.
Infine, dopo lo scavo e il getto della parete destra, i valori di cedimento accumulato superano il 95% in entrambi i modelli, come mostrato nella Figura 7.
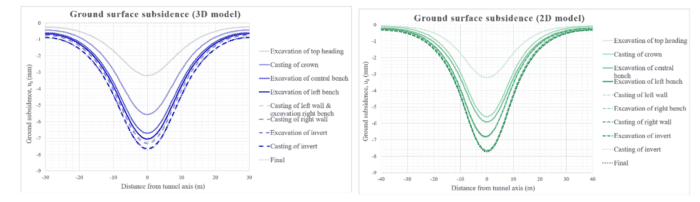
Figura 5 – Cedimento superficiale del terreno nei modelli in ciascuna fase di calcolo
Per quanto riguarda i movimenti verticali della volta del tunnel, il valore raggiunto nella fase finale è pari a:
10,7 mm per il modello 3D,
e 10,4 mm per il modello 2D (vedi Figura 8).
Il movimento verticale massimo risulta correttamente rappresentato durante la fase di scavo della volta (top heading), con valori di:
5,2 mm per il modello 3D,
e 4,7 mm per il modello 2D.
Durante la fase di getto del calcestruzzo della volta (crown casting), il cedimento massimo ottenuto nel modello 3D è pari a 5,4 mm, mentre nel modello 2D risulta 8,1 mm.
Questa differenza nei valori degli spostamenti verticali si riduce progressivamente nelle fasi successive:
nella fase di scavo della panca sinistra, il risultato è 10,0 mm per il 3D e 9,4 mm per il 2D;
nella fase di scavo dell’invert, i valori raggiungono 10,6 mm per il 3D e 10,4 mm per il 2D,
fino ad arrivare, nella fase finale, a una differenza inferiore a 0,3 mm tra i due modelli.
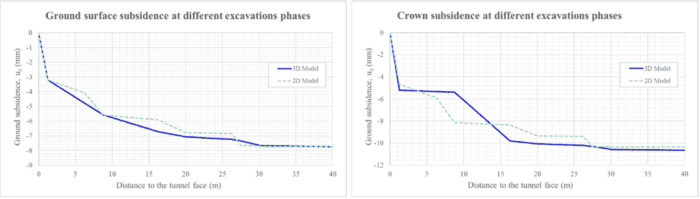
Figura 6 – Cedimenti superficiali del terreno nei modelli in ciascuna fase di calcolo
Sollecitazioni interne nel rivestimento del tunnel
Le forze interne sviluppate nel rivestimento del tunnel sono state analizzate nella fase finale del calcolo, ossia quando l’intera sezione risulta completata con il calcestruzzo di 7 giorni in tutto il rivestimento.
Il grafico seguente mostra i valori massimi e minimi delle tensioni registrate nella volta (crown) e nelle pareti laterali del tunnel.
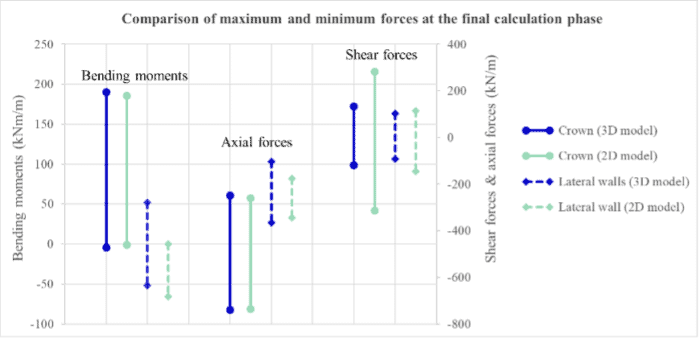
Figura 7 – Forze massime e minime nei modelli nella fase finale di calcolo
Discussione dei risultati
In primo luogo, i cedimenti ottenuti in superficie risultano praticamente identici nella fase finale del calcolo: ciò è confermato dal fatto che l’errore relativo è pari solo allo 0,13%.
Anche la calibrazione nelle fasi iniziali di calcolo risulta ben eseguita, con un errore relativo inferiore all’1%.
A partire dalla fase di getto della parete laterale destra, la variazione dei cedimenti superficiali diventa praticamente trascurabile, e l’errore relativo non supera l’1%.
In generale, quindi, l’adattamento del modello rispetto ai cedimenti superficiali risulta molto accurato in tutte le fasi analizzate.
In secondo luogo, i movimenti verticali della volta del tunnel sono ben calibrati sia nella prima fase di scavo, sia a partire dalla fase di getto della parete laterale destra fino al termine della costruzione.
Nella fase finale, l’errore relativo è pari al 2,8%, corrispondente a una differenza di 0,3 mm.
L’andamento di tali movimenti mostra un comportamento leggermente diverso solo nelle fasi intermedie, ma senza scostamenti significativi.
Infine, le forze interne nel rivestimento del tunnel nella fase finale del modello risultano anch’esse ben calibrate.
Nella volta, i massimi errori assoluti per ciascun tipo di sollecitazione sono:
4,5 kNm/m per i momenti flettenti,
11,6 kN/m per le forze assiali,
148 kN/m per le forze di taglio.
Sebbene, nel caso delle tensioni di taglio, l’errore risulti più elevato, esso rappresenta comunque il valore massimo assoluto e, in ogni caso, le forze di taglio non sono normalmente determinanti nel dimensionamento, a causa del notevole spessore del rivestimento in calcestruzzo.
Per quanto riguarda invece le pareti laterali, l’accordo tra i modelli è meno preciso rispetto alla volta.
Gli errori assoluti riscontrati sono:
52 kNm/m per i momenti flettenti,
72 kN/m per le forze assiali,
54 kN/m per le forze di taglio.
Questa discrepanza può essere attribuita alla diversa simulazione della sequenza costruttiva, poiché la principale differenza tra i modelli 2D e 3D risiede nella modalità di scavo delle panche laterali:
nel modello 2D, ciascuna parete viene scavata e gettata in fasi separate (4 in totale), mentre nel modello 3D lo scavo di una parete è sfalsato temporalmente rispetto al getto dell’altra.
Nonostante ciò, l’accordo complessivo ottenuto tra i due modelli è considerato soddisfacente ai fini dell’analisi.
Conclusioni
In questo studio è stata eseguita una calibrazione di un approccio bidimensionale (2D) di Interazione Suolo-Struttura (SSI) applicato al Metodo Tradizionale di Madrid (MTM).
A tale scopo, sono stati sviluppati due modelli:
un modello 3D SSI, con una sequenza costruttiva complessa e elementi strutturali dettagliati,
e una versione 2D semplificata dello stesso.
La calibrazione del modello 2D è stata condotta confrontando i movimenti del terreno e le forze interne nel rivestimento in calcestruzzo ottenute dal modello 3D con quelle calcolate nel modello 2D.
Dallo studio sono state tratte le seguenti conclusioni principali:
Il parametro numerico Mstage del software PLAXIS 2D consente di simulare con precisione il comportamento di confinamento che si verifica negli scavi tridimensionali, permettendo di riprodurlo in modo realistico anche nei modelli bidimensionali.
Le fasi di calcolo descritte in questo documento riproducono fedelmente il comportamento del Metodo Tradizionale di Madrid (TMM).
La fase di scavo e sostegno della volta (top heading) può essere simulata con due fasi: la prima con un livello di rilassamento del 79%, seguita da una fase virtuale con rilassamento del 40%.
Lo scavo delle pareti laterali può essere rappresentato con un rilassamento del 48%.
Le conclusioni e raccomandazioni presentate in questo studio possono essere utilizzate con competenza e cautela nelle fasi preliminari di progetti simili che impiegano il Metodo Tradizionale di Madrid.
I risultati ottenuti sono stati validati attraverso la letteratura tecnica; tuttavia, si raccomanda di approfondire ulteriormente tali risultati durante la fase costruttiva, mediante analisi a posteriori (back analysis) basate sui dati di monitoraggio in sito.
Riferimenti bibliografici
Melis Maynar, M. (2012). Apuntes de introducción al proyecto y construcción de túneles y metros en suelos y rocas blandas o muy rotas. La construcción del Metro de Madrid y la M-30. Universidad Politécnica de Madrid (UPM).
Rodríguez, J.M. (2000). Propiedades geotécnicas de los suelos de Madrid. Revista de Obras Públicas, Extraordinario – Dicembre 2000, Nº 3405: 59–84.
López Jimeno, C. et al. (2011). Manual de túneles y obras subterráneas (Vol. 1 e 2). Universidad Politécnica de Madrid (UPM).
Cabral Dias, C.; Gonzalez Villavicencio, A.; Masagué Martín, J. (2023). The Traditional Method of Madrid – a 2D SSI approach calibrated via 3D modelling. World Tunnel Congress 2023, Atene, Grecia.

